Journal Articles
In Review
-
20. Reversibility, Chaos, and Attractors in Periodically Sheared Elastic Filaments
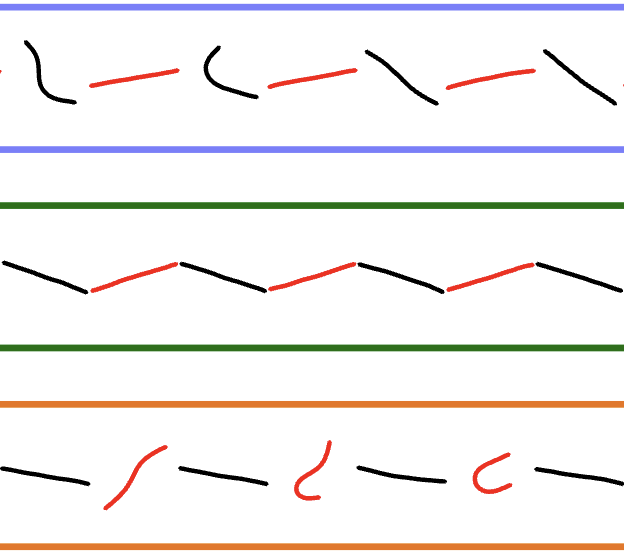
ArXiv, In Review
The dynamics of filaments in flow are central to understanding a wide range of biological and softmatter systems, yet their behavior under time-dependent forcing remains poorly understood. Here, we investigate the long-time dynamics of Brownian inextensible elastic filaments subjected to strong uniform oscillatory shear by combining microfluidic experiments on actin filaments with numerical simulations based on a fluctuating Euler-Bernoulli elastica model in a viscous fluid. As the oscillation period increases, irreversibility emerges from the interplay of flow-induced deformations and thermal noise. This leads to a departure from reversible, deterministic rigid-body dynamics: in this regime, the filaments cycle between nearly straight, flow-aligned conformations at full periods and buckled shapes at half periods. Owing to the time-glide symmetry of the system, two such attracting states in fact coexist with a phase shift of half a period. The system spontaneously selects one, but occasionally switches between them as a result of noise, producing intermittent transitions between apparent order and disorder. This system constitutes an experimentally accessible realization of stochastic symmetry breaking, attractor hopping, and intermittency in a minimal nonequilibrium soft-matter system, with novel implications for the design and control of soft matter systems under time-dependent flows.
-
19. The physical consequences of sperm gigantism
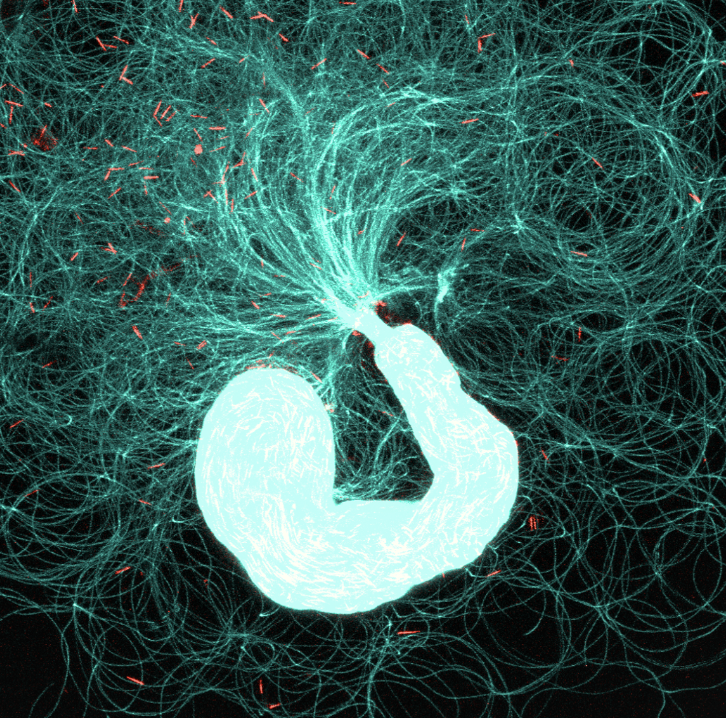
ArXiv, In Review
The male fruit fly produces ~1.8 mm long sperm, thousands of which can be stored until mating in a ~200 micron sac, the seminal vesicle. While the evolutionary pressures driving such extreme sperm (flagellar) lengths have long been investigated, the physical consequences of their gigantism are unstudied. Through high-resolution three-dimensional reconstructions of in vivo sperm morphologies and rapid live imaging, we discovered that stored sperm are organized into a dense and highly aligned state. The packed flagella exhibit system-wide collective 'material' flows, with persistent and slow-moving topological defects; individual sperm, despite their extraordinary lengths, propagate rapidly through the flagellar material, moving in either direction along material director lines. To understand how these collective behaviors arise from the constituents' nonequilibrium dynamics, we conceptualize the motion of individual sperm as topologically confined to a reptation-like tube formed by its neighbors. Therein, sperm propagate through observed amplitude-constrained and internally driven flagellar bending waves, pushing off counter-propagating neighbors. From this conception, we derive a continuum theory that produces an extensile material stress that can sustain an aligned flagellar material. Experimental perturbations and simulations of active elastic filaments verify our theoretical predictions. Our findings suggest that active stresses in the flagellar material maintain the sperm in an unentangled, hence functional state, in both sexes, and establish giant sperm in their native habitat as a novel and physiologically relevant active matter system.
-
18. Breathe in, breathe out: Bacterial density determines collective migration in aerotaxis

bioRxiv, In Review
Bacteria navigate their environment by biasing their swimming direction toward beneficial chemicals and away from harmful ones. Out of all the chemicals bacteria respond to, oxygen stands out due to its ubiquitous presence, distinct influence on bacterial metabolism and motility, and historical role in chemotaxis research. However, a coherent understanding of bacterial motility in oxygen gradients, known as aerotaxis, remains elusive, as evidenced by conflicting reports on the migration direction of the model organism Escherichia coli in self-generated oxygen gradients. Here, by combining experiments, simulations, and theory, we provide a unified framework elucidating the fundamental biophysical principle governing bacterial aerotaxis. We track the migration of bacteria in a capillary channel under self-generated oxygen gradients and show that the migration direction depends on the overall bacterial density. At high densities, bacteria migrate toward regions of higher oxygen concentration, whereas at low densities, they move in the opposite direction. We identify a critical bacterial density at which collective migration ceases, despite the presence of oxygen gradients. A kinetic theory, based on the assumption that bacteria seek an optimal oxygen concentration, is then developed to quantitatively explain our experimental findings. We validate this hypothesis by demonstrating the biased movement of individual bacteria in a dense suspension and proposing a signaling pathway that enables this behavior. Thus, by bridging the molecular level understanding of the signaling pathway, the motility of single bacteria in oxygen gradients, and the collective population dynamics shaped by oxygen diffusion and consumption, our study provides a comprehensive understanding of aerotaxis, addressing the long-standing controversy over how bacteria response to non-uniform oxygen distributions pervasive in microbial habitats.
2026
-
17. Hydrodynamic instabilities in driven chiral suspensions

Physical Review E Letters, 2026
Active Stokesian suspensions are conventionally understood to generate dipolar stresses that destabilize aligned states in the bulk and drive system-wide spatiotemporally chaotic flows. Here, we report dynamics in suspensions of torque-driven spinning chiral particles that exhibit a distinct and previously unrecognized route to collective dynamics. Using a mean-field kinetic theory, stability analysis, and nonlinear simulations, we demonstrate how flows driven by torque monopoles and self-propulsion resulting from microscopic chirality drive chaotic flows in three dimensions. Unlike the well-known alignment instability of dipolar active matter, the present dynamics is intrinsically tied to self-propulsion and relies on the emergent coupling between nematic and polar order. Our results establish a novel route to pattern formation, suggest strategies for designing torque-driven active suspensions, and provide a mechanistic framework to probe the rheology of chiral fluids.
2025
-
16. Geometric Effects in Large Scale Intracellular Flows
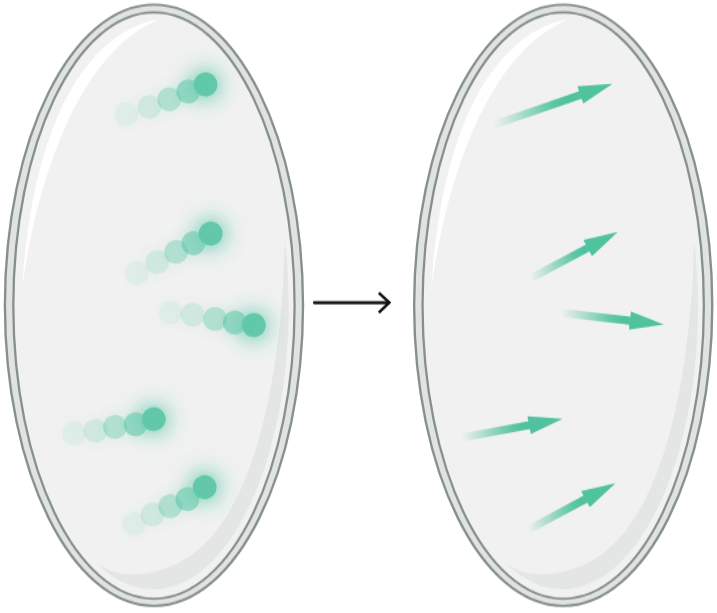
PRX Life, 2025
This work probes the role of cell geometry in orienting self-organized fluid flows in the late-stage Drosophila oocyte. Recent theoretical work has shown that a model, which relies only on hydrodynamic interactions of flexible, cortically anchored microtubules and the mechanical loads from molecular motors moving upon them, is sufficient to generate observed flows. While the emergence of flows has been studied in spheres, oocytes change shape during streaming, and it was unclear how robust these flows are to the geometry of the cell. Here we use biophysical theory and computational analysis to investigate the role of geometry and find that the axis of rotation is set by the shape of the domain and that the flow is robust to biologically relevant perturbations of the domain shape. Using live imaging and three-dimensional flow reconstruction, we test the predictions of the theory/simulation, finding consistency between the model and live experiments, further demonstrating a geometric dependence on flow direction in late-stage Drosophila oocytes.
2024
-
15. Cytoplasmic stirring by active carpets
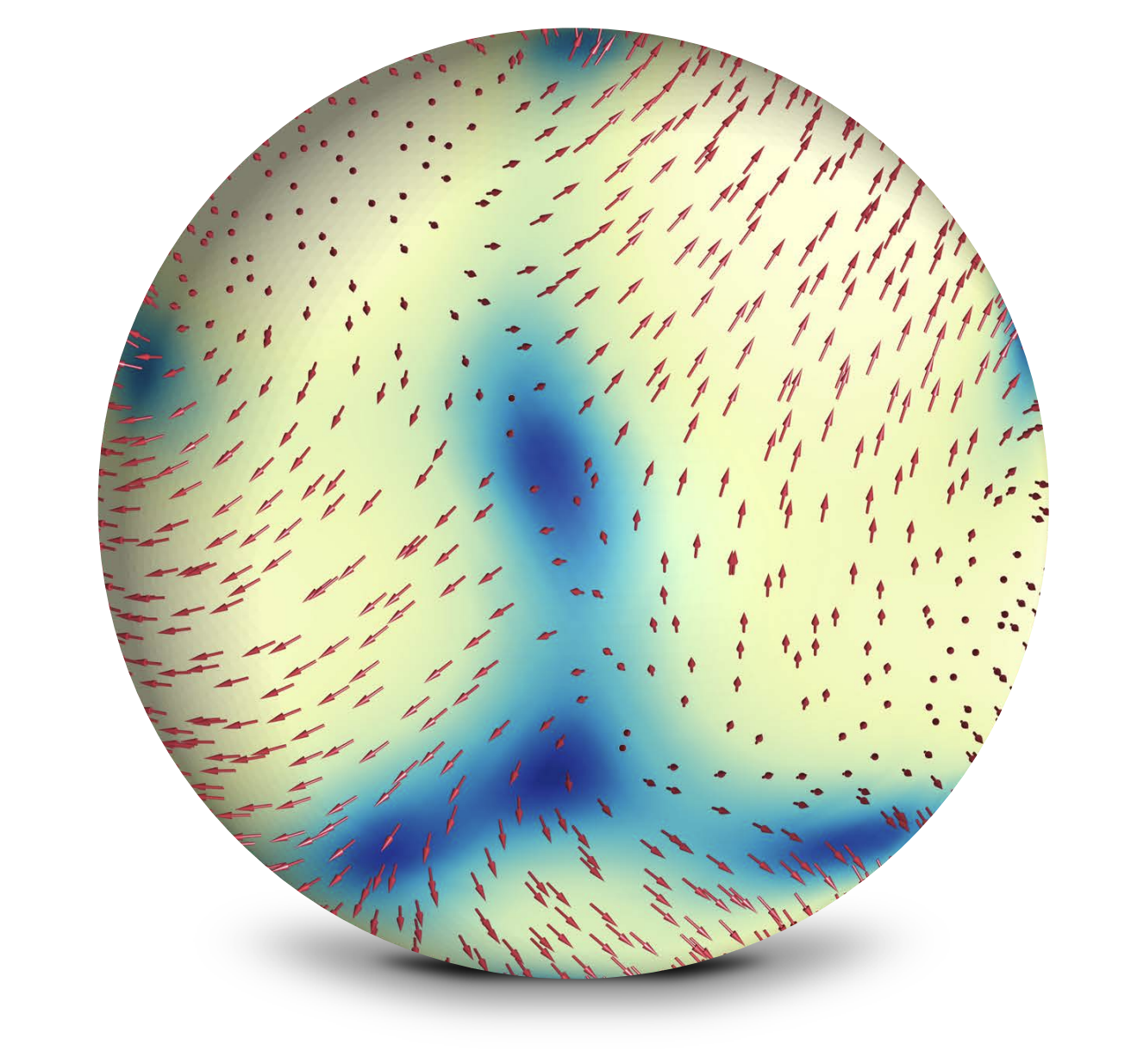
Proceedings of the National Academy of Sciences, 2024
★Coverage by ICTS
In the egg cells of the fruit fly, Drosophila melanogaster, the emergence of cytoplasmic streaming presents a multiscale challenge that intersects developmental biology, transport phenomena, and nonequilibrium physics. The mechanics through which molecular machines orchestrate the robust intracellular streaming flow are highly complex. Here, we distill the key minimal ingredients driving this emergent dynamics by formulating a coarse-grained active carpet theory. Combining mathematical analysis, computations, and nonlinear theory, we reveal the topologies of these flows and illuminate how a complex, high-dimensional system always settles on a low-dimensional global attractor for swirling flows. Our findings unravel various universal aspects of fluid-mediated collective dynamics with potential implications for understanding cellular transport in other large cells.
2023
-
14. Chemomechanical model of sperm locomotion reveals two modes of swimming
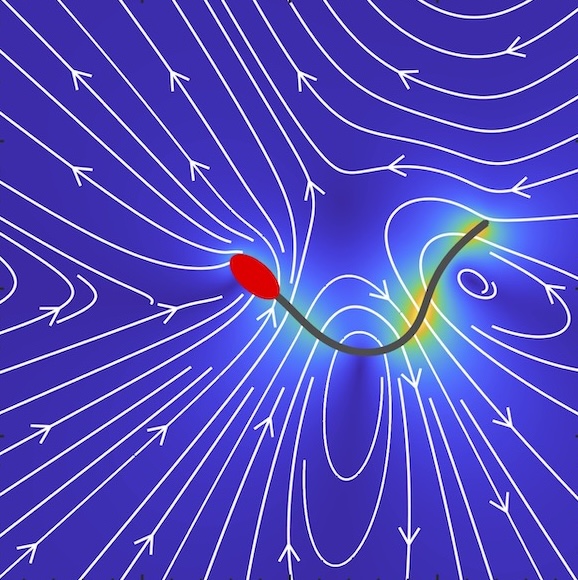
Physical Review Fluids, 2023
★Editor Suggestion, Physical Review Fluids. Featured in UC San Diego Today
The propulsion of mammalian spermatozoa relies on the spontaneous periodic oscillation of their flagella. These oscillations are driven internally by the coordinated action of ATP-powered dynein motors that exert sliding forces between microtubule doublets, resulting in bending waves that propagate along the flagellum and enable locomotion. We present an integrated chemomechanical model of a freely swimming spermatozoon that uses a sliding-control model of the axoneme capturing the two-way feedback between motor kinetics and elastic deformations while accounting for detailed fluid mechanics around the moving cell. We develop a robust computational framework that solves a boundary integral equation for the passive sperm head alongside the slender-body equation for the deforming flagellum described as a geometrically nonlinear internally actuated Euler-Bernoulli beam, and captures full hydrodynamic interactions. Nonlinear simulations are shown to produce spontaneous oscillations with realistic beating patterns and trajectories, which we analyze as a function of sperm number and motor activity. Our results indicate that the swimming velocity does not vary monotonically with dynein activity, but instead displays two maxima corresponding to distinct modes of swimming, each characterized by qualitatively different wave forms and trajectories. Our model also provides an estimate for the efficiency of swimming, which peaks at low sperm number.
-
13. Collective motion and pattern formation in phase-synchronizing active fluids

Physical Review Letters, 2023
Many active particles, such as swimming micro-organisms or motor proteins, do work on their environment by going though a periodic sequence of shapes. Interactions between particles can lead to synchronization of their duty cycles. Here, we study the collective dynamics of a suspension of active particles coupled through hydrodynamics. We find that at high enough density the system transitions to a state of collective motion by a mechanism that is distinct from other instabilities in active matter systems. Second, we demonstrate that the emergent nonequilibrium states feature stationary chimera patterns in which synchronized and phase-isotropic regions coexist. Third, we show that in confinement, oscillatory flows and robust unidirectional pumping states exist, and can be selected by choice of alignment boundary conditions. These results point toward a new route to collective motion and pattern formation and could guide the design of new active materials.
-
12. Dynamics of flexible filaments in oscillatory shear flows

Journal of Fluid Mechanics, 2023
The fluid–structure interactions between flexible fibres and viscous flows play an essential role in various biological phenomena, medical problems and industrial processes. Of particular interest is the case of particles transported freely in time-dependent flows. This work elucidates the dynamics and morphologies of actin filaments under oscillatory shear flows by combining microfluidic experiments, numerical simulations and theoretical modelling. Our work reveals that, in contrast to steady shear flows, in which small orientational fluctuations from a flow-aligned state initiate tumbling and deformations, the periodic flow reversal allows the filament to explore many different configurations at the beginning of each cycle. Investigation of filament motion during half time periods of oscillation highlights the critical role of the initial filament orientation on the emergent dynamics. This strong coupling between orientation and deformation results in new deformation regimes and novel higher-order buckling modes absent in steady shear flows. The primary outcome of our analysis is the possibility of suppression of buckling instabilities for certain combinations of the oscillation frequency and initial filament orientation, even in very strong flows. We explain this unusual behaviour through a weakly nonlinear Landau theory of buckling, in which we treat the filaments as inextensible Brownian Euler–Bernoulli rods whose hydrodynamics is described by local slender-body theory.
2022
-
11. Fluid circulation driven by collectively organized metachronal waves in swimming T. aceti nematodes
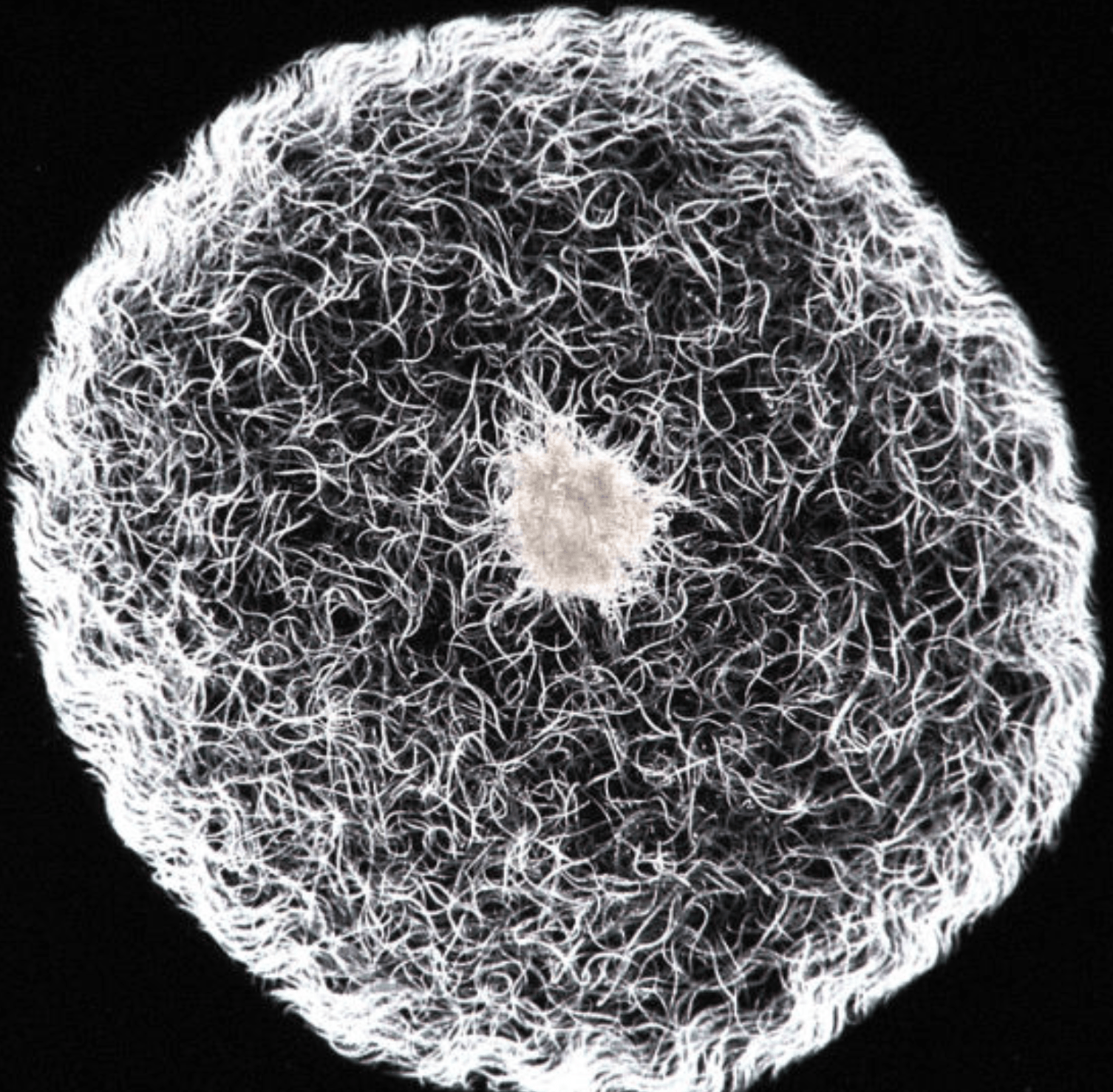
Physical Review E, 2022
Recent experiments have shown that the nematode T. aceti can assemble into collectively undulating groups at the edge of fluid drops. This coordinated state consists of metachronal waves and drives fluid circulation inside the drop. We find that the circulation velocity is about 2 mm/s and nearly half the speed of the metachronal wave. We develop a quasi-two-dimensional hydrodynamics model using the Stokes flow approximation. The periodic motion of the nematodes constitute our moving boundary condition that drives the flow. Our model suggests that large-amplitude excursions of the nematode tails produce the fluid circulation. We discuss the constraints on containers that would enhance fluid motion, which could be used in the future design of on demand flow generating systems.
-
10. A multiscale biophysical model gives quantized metachronal waves in a lattice of beating cilia

Proceedings of the National Academy of Sciences, 2022
★Coverage by the Simons Foundation
Motile cilia are slender, hair-like cellular appendages that spontaneously oscillate under the action of internal molecular motors and are typically found in dense arrays. These active filaments coordinate their beating to generate metachronal waves that drive long-range fluid transport and locomotion. Until now, our understanding of their collective behavior largely comes from the study of minimal models that coarse grain the relevant biophysics and the hydrodynamics of slender structures. Here we build on a detailed biophysical model to elucidate the emergence of metachronal waves on millimeter scales from nanometer-scale motor activity inside individual cilia. Our study of a one-dimensional lattice of cilia in the presence of hydrodynamic and steric interactions reveals how metachronal waves are formed and maintained. We find that, in homogeneous beds of cilia, these interactions lead to multiple attracting states, all of which are characterized by an integer charge that is conserved. This even allows us to design initial conditions that lead to predictable emergent states. Finally, and very importantly, we show that, in nonuniform ciliary tissues, boundaries and inhomogeneities provide a robust route to metachronal waves.
2021
-
9. Signatures of elastoviscous buckling in the dilute rheology of stiff polymers
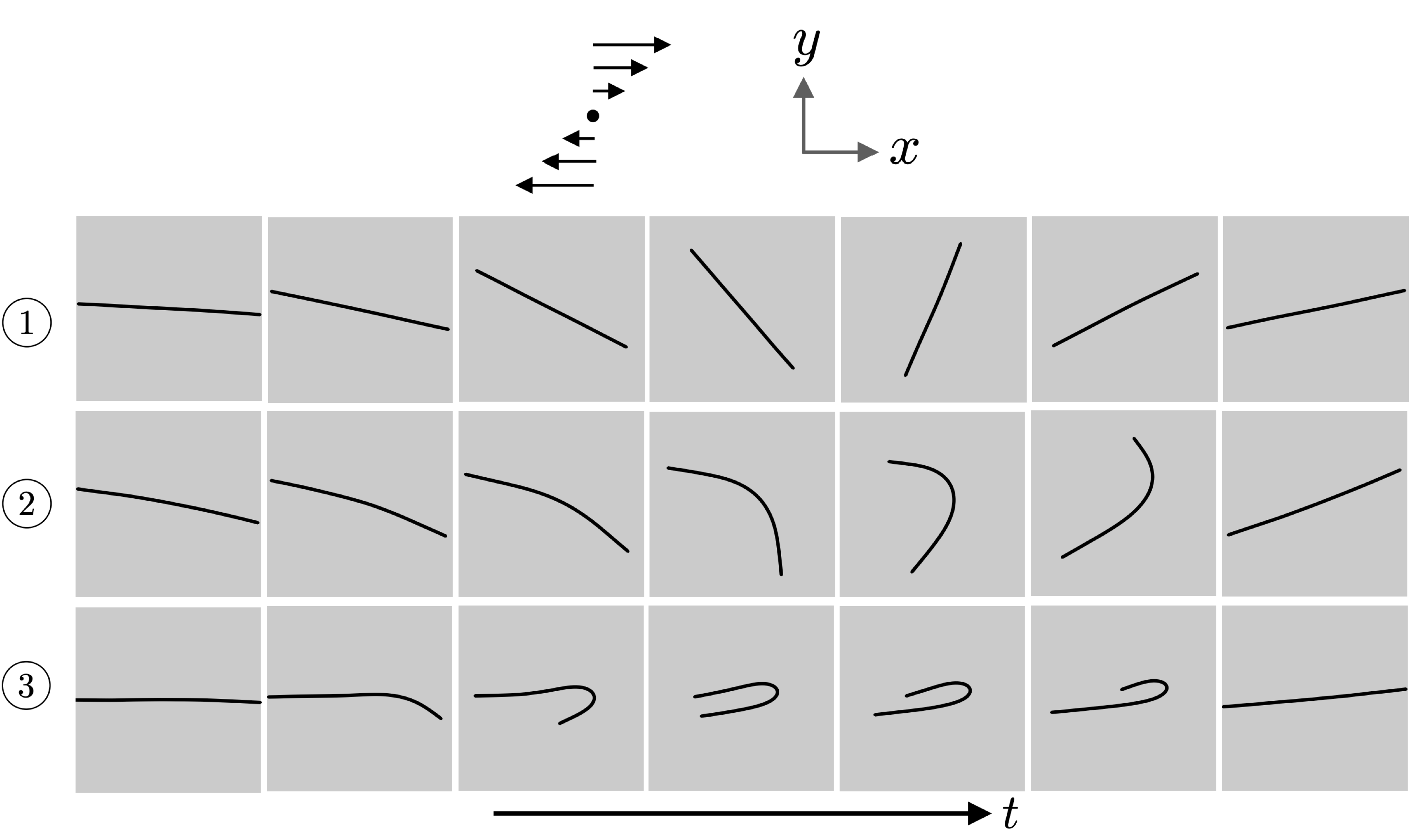
Journal of Fluid Mechanics, 2021
As a stiff polymer tumbles in shear flow, it experiences compressive viscous forces that can cause it to buckle and undergo a sequence of morphological transitions with increasing flow strength. We use numerical simulations to uncover the effects of these transitions on the steady shear rheology of a dilute suspension of stiff polymers. Our results agree with classic scalings for Brownian rods in relatively weak flows but depart from them above the buckling threshold. Signatures of elastoviscous buckling include enhanced shear thinning and an increase in the magnitude of normal stress differences. We discuss our findings in the light of past work on rigid Brownian rods and non-Brownian elastic fibres and highlight the subtle role of thermal fluctuations in triggering instabilities.
2020
-
8. Shear-induced dispersion in peristaltic flow
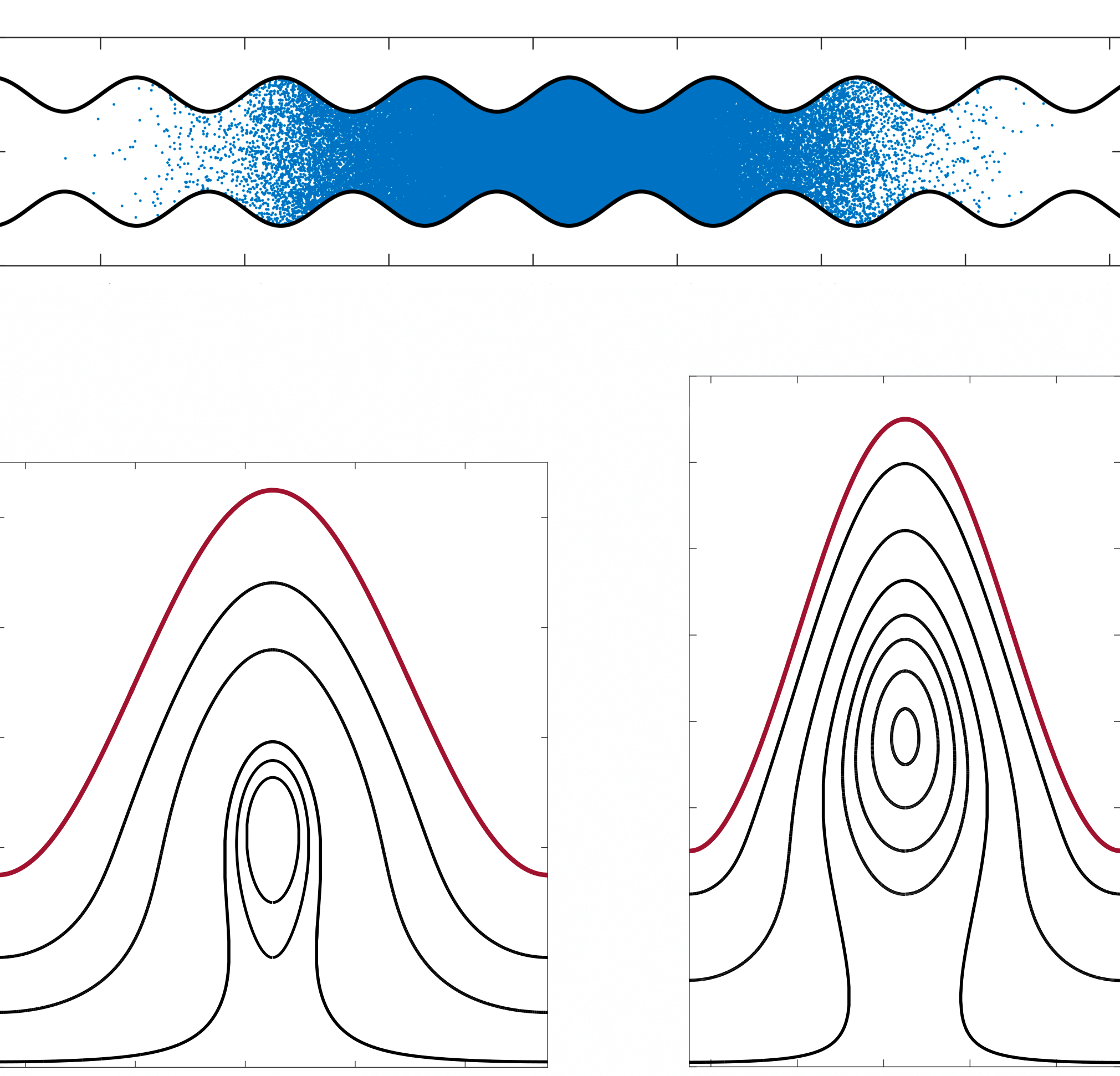
Physics of Fluids, 2020
★Invited, “Contributions from Early Career Researchers 2020”
The effective diffusivity of a Brownian tracer in unidirectional flow is well known to be enhanced due to shear by the classic phenomenon of Taylor dispersion. At long times, the average concentration of the tracer follows a simplified advection–diffusion equation with an effective shear-dependent dispersivity. In this work, we make use of the generalized Taylor dispersion theory for periodic domains to analyze tracer dispersion by peristaltic pumping. In channels with small aspect ratios, asymptotic expansions in the lubrication limit are employed to obtain analytical expressions for the dispersion coefficient at both small and high Péclet numbers. Channels of arbitrary aspect ratios are also considered using a boundary integral formulation for the fluid flow coupled to a conservation equation for the effective dispersivity, which is solved using the finite-volume method. Our theoretical calculations, which compare well with results from Brownian dynamics simulations, elucidate the effects of channel geometry and pumping strength on shear-induced dispersion. We further discuss the connection between the present problem and dispersion due to Taylor's swimming sheet and interpret our results in the purely diffusive regime in the context of Fick–Jacobs theory. Our results provide the theoretical basis for understanding passive scalar transport in peristaltic flow, for instance, in the ureter or in microfluidic peristaltic pumps.
-
7. Trapping, gliding, vaulting: Transport of semiflexible polymers in periodic post arrays
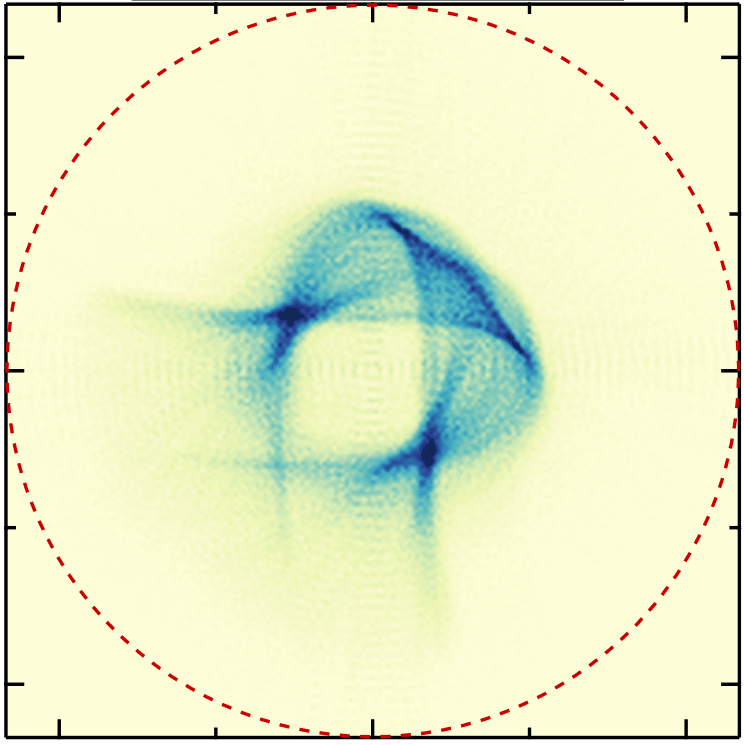
Soft Matter, 2020
The transport of deformable particles through porous media underlies a wealth of applications ranging from filtration to oil recovery to the transport and spreading of biological agents. Using direct numerical simulations, we analyze the dynamics of semiflexible polymers under the influence of an imposed flow in a structured two-dimensional lattice serving as an idealization of a porous medium. This problem has received much attention in the limit of reptation and for long-chain polymer molecules such as DNA that are transported through micropost arrays for electrophoretic chromatographic separation. In contrast to long entropic molecules, the dynamics of elastic polymers results from a combination of scattering with the obstacles and flow-induced buckling instabilities. We identify three dominant modes of transport that involve trapping, gliding and vaulting of the polymers around the obstacles, and we reveal their essential features using tools from dynamical systems theory. The interplay of these scattering dynamics with transport and deformations in the imposed flow results in the long-time asymptotic dispersion of the center of mass, which we quantify in terms of a hydrodynamic dispersion tensor. We then discuss a simple yet efficient chromatographic device that exploits the competition between different modes of transport to sort filaments in a dilute suspension according to their lengths.
-
6. Flexible filaments buckle into helicoidal shapes in strong compressional flows
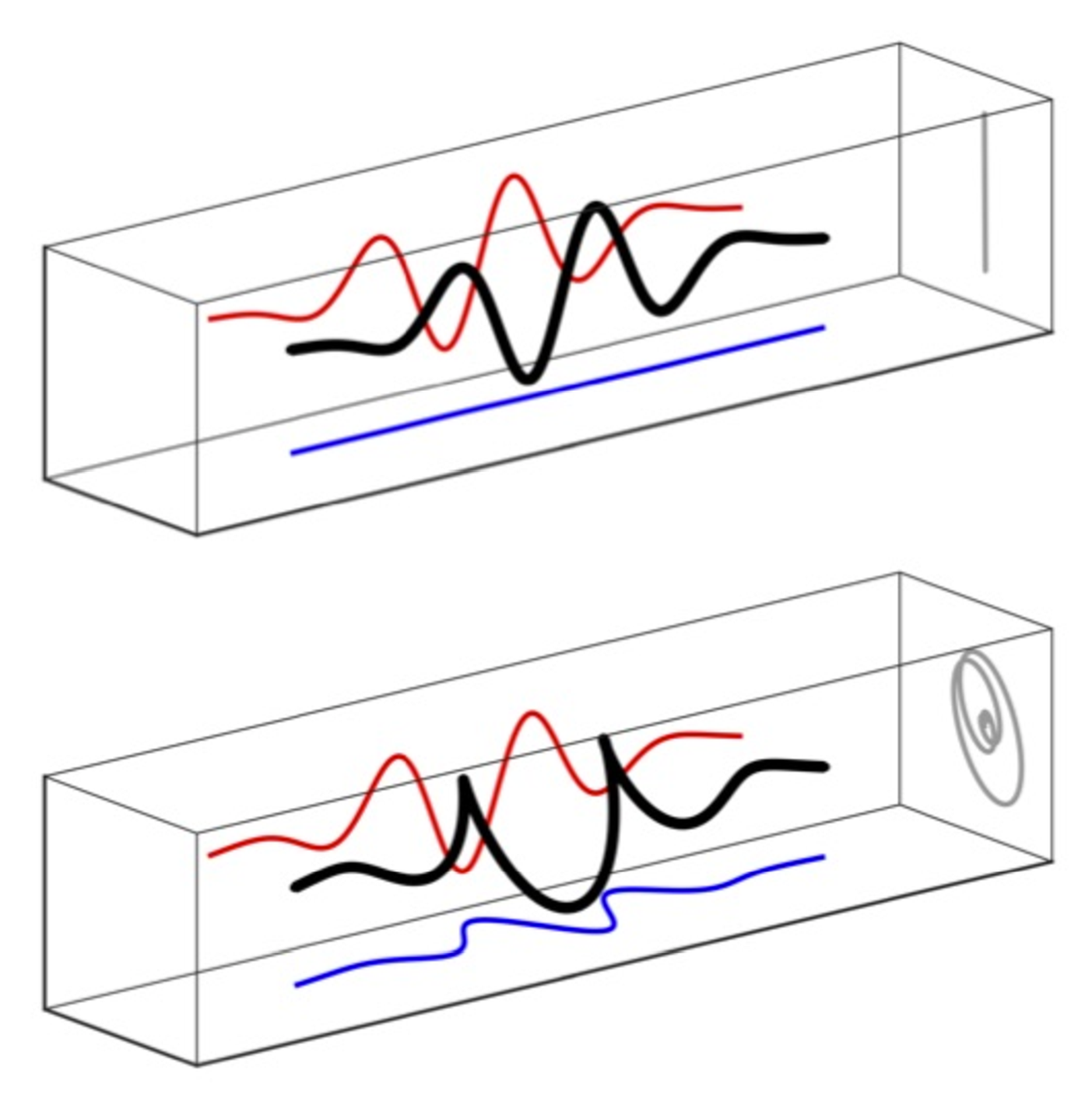
Nature Physics, 2020
The occurrence of coiled or helical morphologies is common in nature, from plant roots to DNA packaging into viral capsids, as well as in applications such as oil drilling processes. In many examples, chiral structures result from the buckling of a straight fibre either with intrinsic twist or to which end moments have been applied in addition to compression forces. Here, we elucidate a generic way to form regular helicoidal shapes from achiral straight filaments transported in viscous flows with free ends. Through a combination of experiments using fluorescently labelled actin filaments in microfluidic divergent flows and two distinct sets of numerical simulations, we demonstrate the robustness of helix formation. A nonlinear stability analysis is performed, and explains the emergence of such chiral structures from the nonlinear interaction of perpendicular planar buckling modes, an effect that solely requires a strong compressional flow, independent of the exact nature of the fibre or type of flow field. The fundamental mechanism for the uncovered morphological transition and characterization of the emerging conformations advance our understanding of several biological and industrial processes and can also be exploited for the controlled microfabrication of chiral objects.
2019
-
5. Hydrodynamic synchronization of spontaneously beating filaments
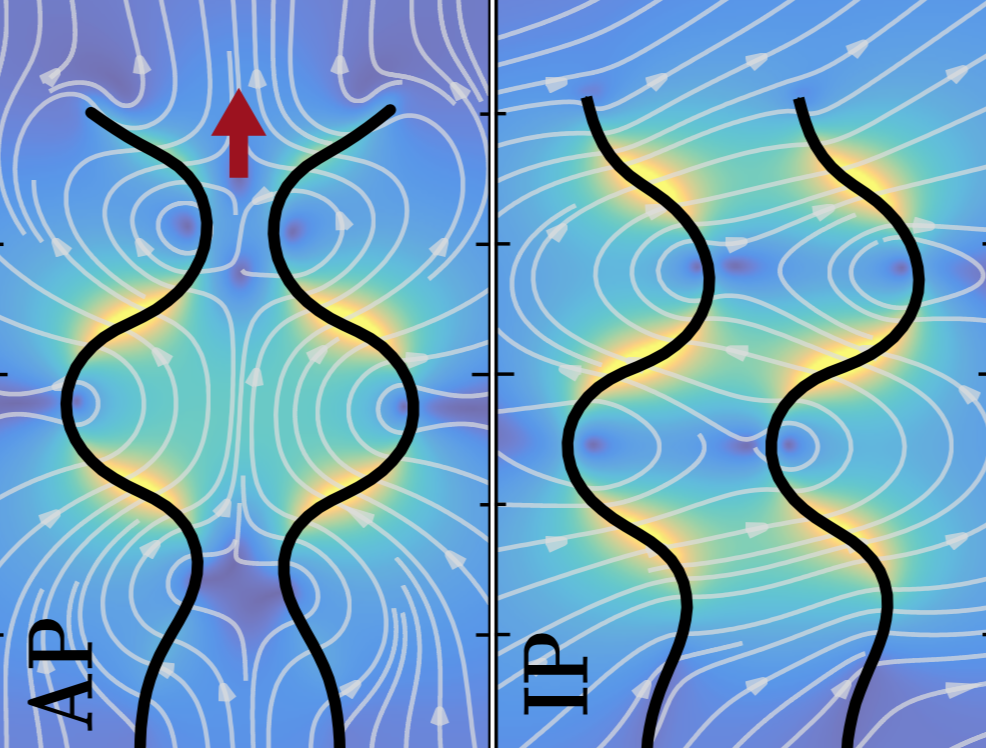
Physical Review Letters, 2019
Using a geometric feedback model of the flagellar axoneme accounting for dynein motor kinetics, we study elastohydrodynamic phase synchronization in a pair of spontaneously beating filaments with waveforms ranging from sperm to cilia and Chlamydomononas. Our computations reveal that both in-phase and antiphase synchrony can emerge for asymmetric beats while symmetric waveforms go in phase, and elucidate the mechanism for phase slips due to biochemical noise. Model predictions agree with recent experiments and illuminate the crucial roles of hydrodynamics and mechanochemical feedback in synchronization.
-
4. Transport and dispersion of active particles in periodic porous media

Physical Review Fluids, 2019
The transport of self-propelled particles such as bacteria and phoretic swimmers through crowded heterogeneous environments is relevant to many natural and engineering processes, from biofilm formation and contamination processes to transport in soils and biomedical devices. While there has been experimental progress, a theoretical understanding of mean transport properties in these systems has been lacking. In this work, we apply generalized Taylor dispersion theory to analyze the long-time statistics of an active self-propelled Brownian particle transported under an applied flow through the interstices of a periodic lattice that serves as an idealization of a porous medium. Our theoretical model, which we validate against Brownian dynamics simulations, is applied to unravel the roles of motility, fluid flow, and lattice geometry on asymptotic mean velocity and dispersivity. In weak flows, transport is dominated by active dispersion, which results from self-propulsion in the presence of noise and is hindered by the obstacles that act as entropic barriers. In strong flows, shear-induced Taylor dispersion becomes the dominant mechanism for spreading, with pillars now acting as regions of shear production that enhance dispersion. The interplay of these two effects leads to complex and unexpected trends, such as a nonmonotonic dependence of axial dispersivity on flow strength and a reduction in dispersion due to swimming activity in strong flows. Brownian dynamics are used to cast light on the preasymptotic regime, where tailed distributions are observed in agreement with recent experiments on motile microorganisms. Our results also highlight the subtle effects of pillar shape, which can be used to control the magnitude of dispersion and to drive a net particle migration in quiescent systems.
-
3. Spontaneous oscillations, beating patterns, and hydrodynamics of active microfilaments

Physical Review Fluids, 2019
Cilia and flagella are ubiquitous in nature and are known to help in transport and swimming at the cellular scale by performing oscillations. Fundamental to these periodic waveforms is the core internal structure of the filaments known as the axoneme, consisting of an array of microtubule doublets, protein linkers, and dynein motors. In the presence of ATP, the collective action of the molecular motors drives internal sliding motions that are converted to spontaneous oscillations by a mechanism that still remains elusive. A sliding controlled axonemal feedback mechanism has recently been proposed and explored in the limit of small deformations, where it was shown to result in nonlinear amplitude selection through a mechanical regulation of dynein kinetics. Here, we build on that model to derive a more complete set of planar nonlinear governing equations that retains all the geometric nonlinearities, incorporates intrinsic biochemical noise and accounts for long-range, nonlocal hydrodynamic interactions. For a clamped filament, motor activity drives a Hopf bifurcation leading to traveling wave solutions that propagate from tip to base, in agreement with previous weakly nonlinear studies. Quite remarkably, our results demonstrate the existence of a second transition far from equilibrium, where nonlinearities cause a reversal in the direction of wave propagation and produce a variety of waveforms that resemble the beating patterns of swimming spermatozoa. We further extend the model to account for asymmetric ciliary beats and also allow for generalized dynein regulation mechanisms that can qualitatively reproduce Chlamydomonas reinhardtii flagellar dynamics. In the spirit of dimensional reduction, limit cycle representations are obtained for various waveforms and highlight the role of biochemical noise. We also analyze the velocity fields generated by the filaments and apply principal component analysis to derive low-order flow representations in terms of fundamental Stokes singularities that could be of use for constructing minimal models of swimming microorganisms.
2018
-
2. Morphological transitions of elastic filaments in shear flow

Proceedings of the National Academy of Sciences, 2018
Elastic filaments and semiflexible polymers occur ubiquitously in biophysical systems and are key components of many complex fluids, yet our understanding of their conformational dynamics under flow is incomplete. Here, we report on experimental observations of actin filaments in simple shear and characterize their various dynamical regimes from tumbling to buckling and snaking. Numerical simulations accounting for elastohydrodynamics as well as Brownian fluctuations show perfect agreement with measurements. Using a reduced-order theoretical model, we elucidate the unexplained mechanism for the transition to snaking. Our results pave the way for a better understanding of biophysical processes, as well as the rheology of sheared soft materials, and provide a theoretical framework for the exploration of the dynamics of dilute and semidilute suspensions.
2016
-
1. Catenaries in viscous fluid
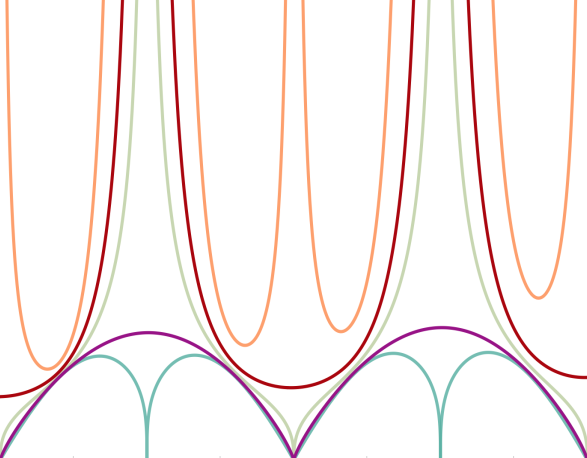
Journal of Fluids and Structures, 2016
This work explores a simple model of a slender, flexible structure in a uniform flow, providing analytical solutions for the translating, axially flowing equilibria of strings subjected to a uniform body force and drag forces linear in the velocities. The classical catenaries are extended to a five-parameter family of curves. A sixth parameter affects the tension in the curves. Generic configurations are planar, represented by a single first order equation for the tangential angle. The effects of varying parameters on representative shapes, orbits in angle-curvature space, and stress distributions are shown. As limiting cases, the solutions include configurations corresponding to 'lariat chains' and the towing, reeling, and sedimentation of flexible cables in a highly viscous fluid. Regions of parameter space corresponding to infinitely long, semi-infinite, and finite length curves are delineated. Almost all curves subtend an angle less than π radians, but curious special cases with doubled or infinite range occur on the borders between regions. Separate transitions in the tension behavior, and counterintuitive results regarding finite towing tensions for infinitely long cables, are presented. Several physically inspired boundary value problems are solved and discussed.